|
|
目次 1 はじめに 付録:電圧の時間変化を観測するオシロスコープ(シンクロスコープ)
|
1 はじめに
図1のように、純銅板の上方から円板形の磁石を落とします。そうすると静かに着地します。この「ふわっと君」と呼ばれる理科実験装置は大阪大学の久保等先生によって考案されたもので、電磁誘導現象を観察、体験できます。試しにこの磁石を手で持って銅の円板に平行を保って銅板にグイと近づけてみてください。反発力を感じると思います。ここでは磁石を銅板の上から落とした時に、磁石がどんな速度で落下するのか、装置を工夫して計測してみましょう。
 |
|
図1「ふわっと君」 |
何を測定するのか、そう、落下中の磁石の高さ(位置)の時間変化とそこでの速度ですね。そして、速度は2つの点(A点とB点)の高さを測り、それぞれの高さを通過した時刻を測定して、
|
速度= |
|
を計算して出すことができます。さらにこの速度の変化から加速度(重力や制動力)を求めることができます。ふわっと着地することは速度が着地前にゼロになることですが、その様子が測定できるでしょうか。
| 注意 この実験では、普通にある磁石とは桁違いに強力な永久磁石を使います。実験を試みる場合は以下の危険性を知って、磁石の取り扱いに十分注意してください。できれば実験のベテランの立ち合いのもとで行うようにしてください。磁石が机の上の鉄の文具を急速に引きつけ、場合によってはナイフが飛んでくることもありえます。2つの磁石がくっついたら、道具がないと離せません。鉄に吸い寄せられた磁石との間に指などを挟まれると怪我をします。手袋で防御してください。磁石が欠けて鋭い角ができたり、割れた磁石片が針のように飛び散る可能性もあります。机の目に見えない釘やボルトに引き寄せられるので、それにも注意。 もうひとつ大事なことですが、磁気カードやクレジットカードの内容を壊す可能性もあります。1m以内にクレジットカードなどがないことを確認してください。 この実験を行う場合は自己責任で行って下さい。 |
2 磁石(永久磁石)
2-1 実験に使う磁石と銅板
「ふわっと君」の実験では図1の磁石と銅板を使いましたが、ここで説明する実験では図2のような純銅の円板と強力な磁石(ネオジム永久磁石)を使います。磁石は直径3.8cm、厚さ1.2cm、重さは109gです。磁石中心、磁石面上での磁界強度は370mT(ミリテスラ)です。銅板は、直径15cm、厚さ0.3cmの銅板を3枚重ねて使います。
 |
|
図2 銅板(上)と永久磁石(下) |
2-2 磁石の磁力線の様子
最初にこの磁石からどんな磁界(磁力線)が出ているのかを調べてみました。それには小さな鉄の粒子である「砂鉄」を使います。その結果が下の図3です。左半分には、写真をもとにして、磁力線を何本か手で書きこんでみました。(砂鉄でこの図をつくるのにもコツがあります。「subaru」[oy1] という名のホームページに書いておきますので、参考にしてください。)
 |
|
|
図3 磁石から出ている磁力線の様子
|
3.落下実験装置
実験では銅板の上方から磁石を水平に保って放し、どのような速度で落ちていくのかを測ろうとします。さて、どんな装置がいいのか、考えてみましょう。
1.まず、何をしたいのか、できるだけ細かく手順を書きあげて見ましょう。
2.その手順を実行するために、どんな仕組み、装置がいいのか、考えてみましょう。
(皆さんは上の1.2 を自分で考えてみましょう。以下は私の考えた手順と測定法です。)
3-1 何をしたいのか
私は以下のように整理してみました。
1)落下させるまで磁石を固定しておく(台の上に載せておくか、吊り下げておく)。
2)落とそうと思った時に(いつでも)落とせるような仕組みにする。
3)磁石が垂直に落ちること。横方向(水平方向)には動かないようにする。
4)磁石が水平なまま、傾いたりしないで落下するように
5)落ちた時に衝撃で磁石が割れないように。
6)何回でも、落下を繰り返せるようにする。
7)(できれば)落下する距離を変えられるようにする。(たとえば、落下する距離を3cm、5cm、10cmなどに変えられるように。)
8)落下する磁石の落下の速度を測れるようにする。
9)速度を測って、それを記録できるようにする。
ところで、みなさんが書いたのはどんなでしたか?最後の9)はたぶん書き落としているでしょうね。「測る」というのは、台秤で重さを測るように針の動きをその時に読み取るだけでは、役に立ちません。測った結果の数字や、電圧の波形を何かの方法で記録して、あとで何回でも見直すことができるようにしておかないと(研究の)役に立ちません。台秤でお芋の重さを測っているときでも、きっと読み取った重さをノートなどに記録しているはずです。記録のない「測定」はありえないと覚えておいてください。
ここで最も難しいのは8)の速度の測定です。いろいろ考えてみてください。
3-2 磁石を銅板の上方の位置から落下させるための装置
同じ位置から磁石を静かに落とす方法にはいろんな案が考えられます。
1) 台から落とす方式(a)台を水平方向に引いて落とす
2) 台から落とす方式(b)台を半分に割れるようにしておいて、台を左右に開いて落とす
3) 磁石に糸をつけて、糸を切って落とす (ナイフで糸を切る/ 火で糸を焼き切る )
4) 電磁石に磁石を吸いつけておいて、電磁石の電流を切って落とす
5) 磁石に糸をつけて、糸の反対側に小さな輪をつけ、輪の中に棒を差し込んで止めておく。
その横棒を引き抜いて落下させる
6) まだいろんな案があるかもしれません。考えてみてください。
いろいろな方法が考えられます。大事なことは、少なくても2つ、できれば3つ以上は、違う方式を考えてみることです。そして、考えた2つ以上の方式について、ここはいいけど、ここはまずい、という比較表を作ってみましょう。
比較するには、なにが実験の上で大事なのかを考えてみることが必要です。いまの場合、そういう装置が作れるのか、作りやすいか、という点も大事な点です。そしてもうひとつ、落下を何回も簡単に繰り返せるかどうか、ということも大事です。どんな実験でも、装置を作ったらすぐに最初からデータがとれるわけではありません。まともなデータがとれるようになるまで、何回も、何日も、繰り返して、不都合なところがあればそこを作り直して、ようやくデータがとれるのです。1回落下させるのにすごい手間がかかるようでは、データがとれるようになるまで、何十日も必要になってしまいます。手軽に、再現性良く落下させることができるか、ということを重視する必要があります。
落下させるときに磁石が傾かないで静かに水平に落ちることも必要です。これはどうしたらできるでしょうか。考えてみてください。
4.測定装置
落下の様子(落下速度)を測る装置についても考えてみましょう。考えられる3つの例を書いておきます。ほかにもいい方法があるかもしれません。
1)落下する様子をビデオカメラで撮影して、あとで撮影した1コマ1コマから位置を読み取る。そのためには、落下コースの隣にものさしを置いておく必要があります。
2)磁石にひもをつけて、繰り出される紐の長さを測る。たとえば、大きな輪(プーリー)に糸を巻き付けておき、プーリーの軸にはバリオーム(注)をつけて、プーリーが回ったらバリオームの抵抗値が変化するので、その抵抗値を測る。
(注)軸を回すとリード線間の電気抵抗値が変化する部品を「バリオーム」といいます。昔のラジオやテレビの音量調節に使っていました。バリアブル(変化できる)とオーム(抵抗)からの造語です。
3)磁石の上にものさしをつけ、落下中に通り過ぎる目盛の数をフォトダイオードなどで読み取る装置を設置しておく。
この3つのうち、2)は、落下する磁石がプーリーを回すのですが、そのために落下が自由落下ではなくなります。銅板の落下への影響を調べる、という目的からは、自由落下である必要は特にないので、この方法もいいかもしれません。プーリーに摩擦装置をつけて、落下速度を一定にすることができれば、この方法が3つのうちで一番実験に適しているかもしれません。
(なお、地球の重力以外の何の力も加わらない落下を「自由落下」と言います。)
きっとほかにも方法があると思うので、考えてみてください。
5.実際に製作して実験に使った例
この論文で製作した装置は図4です。
上に書いた諸案の中で、磁石を吊り上げておいて、吊っている針金の上の端に輪をつけ、輪の中に通した横棒を横に引き出して落下させる、という方法を採用しました。台に乗せると水平のまま落とすのが困難ですし、落下させるとき台を大きく引いたりする構造が難しいと思ったからです。
図4の装置では、最初は緑色の台が一番上だったのですが、一度作った後に、落下距離をすこし増やそうとして高さを継ぎ足したので、緑色の台の上に4本の柱を立てて継ぎ足しています。ちょっと見栄えが悪いですが、実験に困ることはありません。実験には試行錯誤がつきものです。見栄えが悪くても恥じることはありません。(でも、よく考えてよくできた装置は自然にきれいな美しい装置になります。そういう意味で、この写真は、いい例ではないかもしれません。みなさんは、がんばって、もっと見栄えのいい装置を作ってください。)
 |
|
|
図4 磁石落下実験装置
|
下の図5にはこの装置の基本部分の構成を説明してあります。
装置設計のポイントは、
①円形磁石を水平のまま落下させること、
②どれだけ落下したかを計測できるようにすることです。
落下させる磁石の上には、長さ6cmの薄いプラスチックのシートを丸めた筒を接着してあります。一方、垂直な落下コースの周囲4か所にはガイドレールが立ててあり、筒のついた磁石はその中を落下中、水平な姿勢を保って落下します。磁石の直径は3.8cm、ガイドレールは直径4cmの円に沿って設置してあり、磁石とガイドレールの間には薄いプラスチックの円筒があるので、磁石は落下中、ガイドレールには触れません。筒の上部には中心線に沿って長さ20cmの幅7mm、厚さ1mmのものさしが垂直に接着してあります。ものさしに光をあて、落下する目盛の反射光を集光レンズで集めて、その焦点位置にフォトダイオードを置いて検出します。これによって磁石落下中の目盛から光のパルス列(ものさしは白く、目盛りは黒いので、光のマイナス・パルス列)がシンクロスコープに記録されます。パルスの個数をカウントすれば落下位置(落下距離)が分かります。
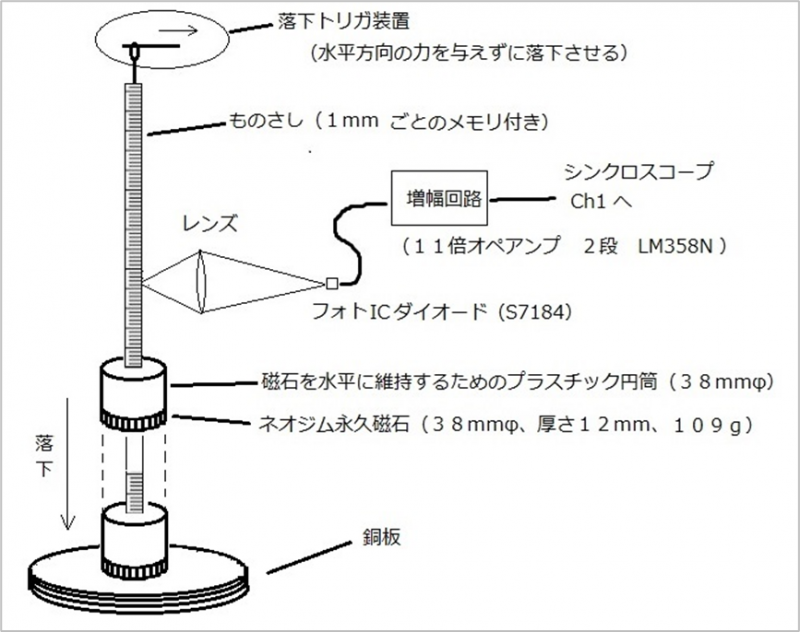 |
| 図5 磁石落下実験装置の基本部分 |
6.実験結果
6-1 実は・・・
次の6-2以降に実験の結果などを書きますが、実はその前に別の方法で測定しようとして2か月かけましたが、うまくいきませんでした。それは、測定に4.の1)に書いた、ビデオカメラを使う方法でした。失敗の原因は、ビデオカメラでは、1)写真を撮った正確な時刻が分からないことと、2)位置の測定もできなかった ためです。1)に対しては、時刻が分かる「時計」を一緒に撮影すれば解決すると思ったのですが、カメラがシャッターを開いている時間が5ms近くあって、1msの精度では時刻を読み取れませんでした。(シャッター開の時間が5msということは、普通のカメラの1/200 の設定に相当します。)また、シャッターが開いている時間が長いために、磁石の位置がぼやけて撮影されてしまい、位置の判定もできませんでした。以下のデータの中に ms(ミリ秒、1/1000秒)単位の時間信号を使っていますが、この回路は実は上記の「時計」として使ったLEDを光らせるために作ったものです。)でも、ビデオカメラを使った試行もいい経験でした。実験に失敗はありません。思った通りにならなくても、くじけずに次の手を試すのが実験です。そのためにも、いろいろなオプションを考えて比較しておくことが大事です。一つ失敗したら、すぐに次のトライに取り掛かれるようになりますから。
皆さんは、テレビで見た超スローモーションの動画を思い出して、「あれと同じにすればよい」と思っているかもしれませんね。それはそれで正しい。でも超スローモーション撮影が可能なビデオカメラは高価です。私たちは自分の頭を使って、安価な実験装置を工夫することもできます。
6-2 オシロスコープ波形と落下距離の計測
ここで採用した方法、フォトダイオード(PD)で光学的にものさしの目盛を測定する方法には、ここではオシロスコープという測定装置を使いました。オシロスコープという単語は馴染みがなく、はじめてかもしれません。最後に付録として説明しているので、それを見てください。また、オシロスコープの波形について、少し詳しい説明を文末に書いた「subaru」に載せてありますので見てください。(4.の2)の場合も落下が1秒以下と速い現象なので、抵抗値の測定にはオシロスコープが必要です。)
実験においては、磁石を高さ約100mmの位置から銅板の上に落下させます。その時のフォトダイオードで測定したものさしの目盛りの信号の例を図6に示します。図6(a)は横軸(時間軸)の1単位(方眼目盛の単位長)が50ms(ミリ秒)で、波形の谷がものさしの黒い目盛りの線に対応しています。図6(b)は、図(a)の横軸(時間軸)を20倍引き伸ばして、細かい変化を見えるようにした図です。1パルスごとに1mm落下しています。パルス信号の間隔がだんだん短くなっていますが、これは重力による加速を示しています。そして図(a)の落下開始から約0.15秒間(150msの間)速い速度で落下し、その後、150msから240msまでは非常にゆっくりした速度で落下して着地したことが分かります。
図6(b)は80msまでの拡大図しか示していませんが、実際には240msまで全部の拡大図を作って約100個の目盛全部について、フォトダイオードで測定している地点を通過した時刻を読み取って、表に記入しています。その値をパソコンのExcel というソフトに打ち込み、グラフにしたり計算処理をしました。
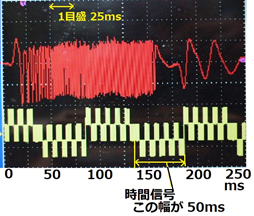 |
|
(a)落下全行程の波形
|
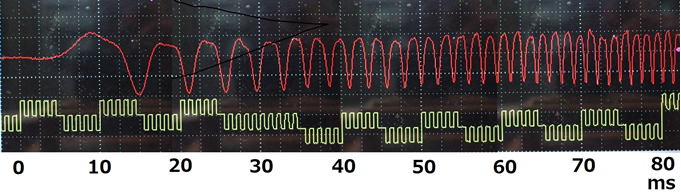 |
|
(b) (a)の0 msから80 msまで取って横軸時間を20倍に拡大(2.5ms / 横軸目盛) 図6 フォトダイオード信号
(a)(b)両図の下半分に出ているのこぎりの歯のような波形は、時間測定を容易にするために入れた時間信号。 |
6-3 測定結果 落下中の高さ、速度、加速度の時間変化
(1)高さ 対 時間
落下開始からの時間(ミリ秒 以下msと記す)と落下距離との測定結果は図7に示すとおりです。この図から、さらに何段階かの計算処理をします。
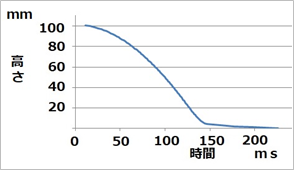 |
| 図7 高さ 対 時間 |
(2)速度 対 時間
図7の高さ対時間のグラフから、隣り合う2つの測定点の値の、位置の差を時間の差で割って速度を出したグラフが図8です。2つの測定点の間の速度の平均値ということになります。その値に対応する時刻は、2つの測定点の時刻の中間点とします。
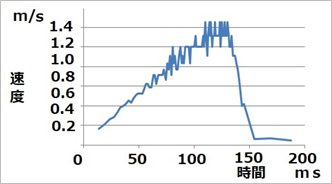 |
| 図8 速度 対 時間 |
100msまでの間、速度はほぼ一定の割合で増加し、100msで約1m/s に達していますが、これは地球の重力加速度(約9.8m/s/s)による加速で、自由落下と呼ばれる状態です。図8の速度対時間のグラフで注目すべき点は、初期の自由落下による加速に続いて140ms付近から減速が始まり、150ms以降に非常な低速となって、落下していることです。
(3)加速度 対 時間
図8の速度のカーブでもう一回、位置から速度を出した方法で計算すると、加速度が時間とともにどのように変化するかが分かります。それを示したのが図9です。
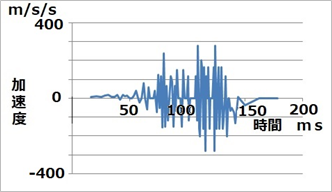 |
| 図9 加速度 対 時間 |
図8の速度のカーブの小さなばらつきが図9に大きく影響して、上下に乱れたカーブとなっています。が、本当はなめらかなカーブであるはずです。そこで、図9のグラフのデータで、各点と両側2点との5点の平均値をとってカーブを滑らかにしたものが図10です。
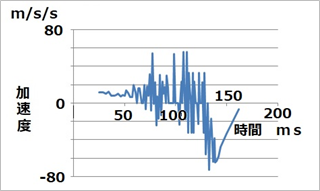 |
| 図10 加速度(5点平滑化)対 時間 |
図10では、縦軸の値が400から80に小さくなって、グラフが上下に5倍拡大されていることに注意してください。最初から50ms付近までの間では、プラス約10 m/s/sの加速度を受けていることが分かります。これは地球の重力加速度です。(プラス・マイナスは、下向けの加速度がプラスになるような決めかたをこの資料では採用しています。)そして、140-150msほどの間ではマイナス側に短時間の間大きな値のパルス的な加速度がありそうです。そのピーク値は60 m/s/s くらいありそうです。
100msまで一定な加速度 約10m/s/s は、地球がものを引き付ける加速度で、「重力加速度」と言います。加速度に質量をかけると「力」ですね。重力加速度が重力、重さを作っています。
そのあと、約130msからは図10でマイナスの値、すなわち重力加速度と反対方向の強い加速度が加わっていることが分かります。この重力と反対方向(上向き)の強い加速度は、銅板の中に生じた誘導電流(渦電流)が作った磁界がネオジム磁石に与えるものです。ほんの20msくらいの短い時間に強い加速度を出すので、衝撃加速度と呼ぶべきものです。が、分かりやすいように、これを「衝撃力」とも呼ぶことがあります。この衝撃加速度は図10で分かるように、地球の重力加速度の6倍の-60 m/s/s にもなる大きな加速度です。地球の重力加速度の倍数で〇G(何ジ―)という言い方をよくしますが、その言い方で言うと、「6Gもの強い上むきの加速度で落下速度を急激に低下させる」です。
7.結果と考察
1)強力な磁石を銅板上に落下させたときの、落下速度の変化を測定することができました。
2)磁石が銅板からまだ遠い距離にある間は、地球の重力加速度(G、ジー)だけで速度が加速されているはずですが、図10で比較的乱れが少ない45msまでの間の加速度の平均値は9.795m/s/s です。東京のGの正確な値は9.796 m/s/s ですから、すごい精度でGが出てきました。こんな簡単な装置で大事な物理定数が高い精度で測れたのは驚きです。(ただし、何個目のデータまでで平均をとるかで、相当違う値が出てしまいますので、高い精度で測れた、という言い方は不正確です。Gの測定という意味では、違う計算法をとるべきでしょう。(文末付録の*印参照)
3)磁石が落下してほとんど銅板に密着しそうになると、すなわち銅板と磁石の距離が5mm以下程度に接近すると、突然、磁石は非常に強い反発力を受けて、減速し、銅板に激突することはありません。その過程での速度の変化を1mmごとに測定することができました。
4)上記の最終段階において、銅板と磁石の間に作用する強い反発力、すなわち衝撃加速度は、地球重力加速度を1Gとするとき、6Gにもなる強い加速度であることが分かりました。(落下距離約10cmで実験した場合)。その結果、磁石は速度を失って低速で銅円板表面に軟着陸します。6Gという加速度は宇宙ロケットや戦闘機レベルの加速度で安全性に心配はありますが、数10ミリ秒のごく短時間のパルス的加速度なので、大丈夫かもしれません。普通の人がこの衝撃力を受ける状況になったら、安全性の検討も十分に行われるでしょう。
なお、150ms以降、着地寸前の数mmについては、1mmごとの目盛データしか取れていません。着地寸前につては、別の方法でもっと詳細なデータをとりたいものです。
5)この実験で明らかになったちょっとした驚きは、磁石減速が銅板に衝突直前になって急激に働くことです。この装置は「ふわっと」と名付けられたように、当初、磁石はフワッと銅板に着地するものと思っていたのですが、そうではなくて、音は出ないもののまず最初に「ガクンと」減速してから「ふわっと」着地する2段階過程であることが明らかになりました。
この接近時の急減速は磁気の反発力の特徴といって良いでしょう。今話題の超電導リニア列車は磁気反発力で浮上しているのですが、その乗り心地は「ふわふわ」というより「かたかた」というようなものです。当然、実用列車においては機械的な緩衝装置を組み合わせて乗り心地を改善する予定と聞いています。
付録:電圧の時間変化を観測するオシロスコープ(シンクロスコープ)
2次元の表示板があって、横軸をx、縦軸をyとして任意の点(x、y)の位置が発光する表示装置(ディスプレー)を持った計測装置です。昔はブラウン管という大きな真空管を使っていましたが 今は液晶が使われています。表示面の横軸をx軸として、xの値は時間とともに増える値を入れ、 縦軸(y軸)に測定しようと思う電圧の時刻tでの値を入れてグラフを描くと y=y(t) の波形を描くことができます。
周期性の現象であればその周期に合わせて横軸の時間をくりかえせば、 周期波形は重なるので止まって見えることになります。また、ここの実験のように1回だけの単発の波形は波形の開始時に合わせて 横軸xを時間tで動かせば良いことになります。このように横軸を波形の出発に合わせることを同期、あるいはトリガーと呼びます。いま販売されているオシロスコープにはトリガー回路が備わっています。トリガー信号は y軸の測定波形の初期変化信号でもいいし、外部から別の信号を入れることでもいいのです。
実験におけるオシロスコープの利用
磁石が10cm落ちるのにかかる時間は1秒以下です。1秒以下の短い時間で起こる現象の様子を正確に測るのにはオシロスコープを用いれば良いわけです。
これは第一線の専門家たちも使っている便利な装置ですが、安いものならば2万円程度で買えます。パソコンにつないでパソコンの画面を使うものもあり、それは1万円以下でも入手できます。オシロスコープの簡単な歴史は以下のサイトに記載されています。
http://www.jemida.jp/column/column02-11.php
 |
| 付図 筆者が使っているオシロスコープ |
これは筆者が使っているオシロスコープです。2015年ころですが、1万5千円でした。非常に高い性能で、光が1m伝わる時間(約3ナノ秒、ナノ秒は、1秒の10億分の1)も測定できます。
画面には、横軸に時間、縦軸に電気信号の電圧をとったグラフを表示します。
装置の右半分は、電圧を1目盛何Vで表示するか、時間は1目盛何秒で表示するか、などを設定するためのボタンやダイアルが付いています。
*ここで報告した実験のより詳細な説明 http://subaru.jakou.com に載せてありますので、ご覧になってください。
「銅板上へ落下する磁石の運動を測定してみよう」
本稿の4章でいう実験結果とは、上記の実験結果ですので、できればこちらを先にご覧下さい。
(専門家の方々への注:以下に示すのは磁石や銅板の大きさや厚さ、材料による透磁率の違い等は無視した簡略化した考察です。)
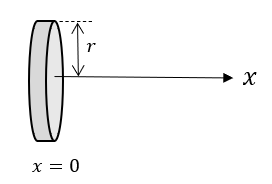 |
| 図1 円盤状磁石 |
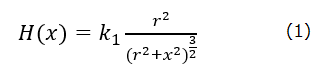
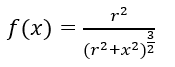 とおきます。ふわっと君の磁石は直径38[mm]ですので、r=19 [㎜]として、f(x) の x に対する変化様相を図示したものが図2です。これを見ると、磁石の直径程度以上磁石から離れると、磁界の強さはかなり弱くなることが判ります。
とおきます。ふわっと君の磁石は直径38[mm]ですので、r=19 [㎜]として、f(x) の x に対する変化様相を図示したものが図2です。これを見ると、磁石の直径程度以上磁石から離れると、磁界の強さはかなり弱くなることが判ります。 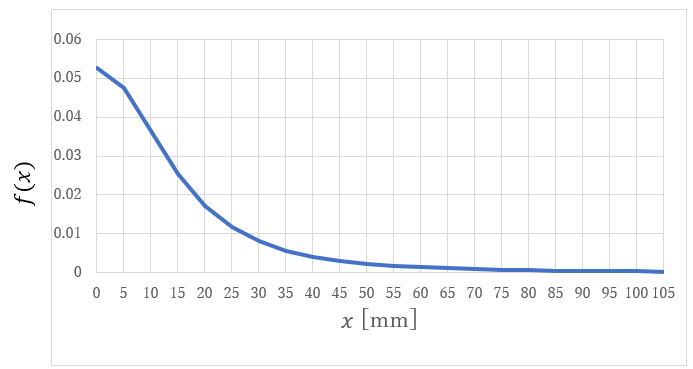 |
| 図2 中心軸上で磁界が変化する姿 |
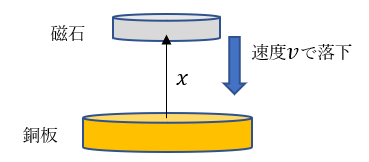 |
| 図3 銅板に落下する磁石 |
3.1 磁石によって銅板内に流れる渦電流
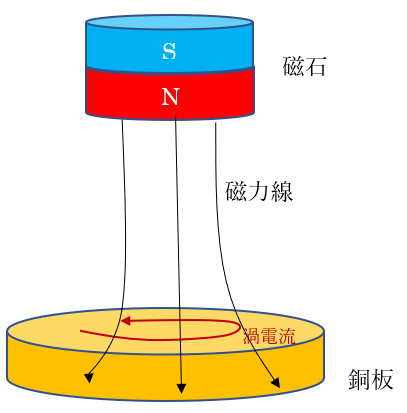 |
| 図4 銅板に流れる渦電流(磁力線、渦電流はイメージ) |
この渦電流の大きさは銅板中の磁束密度Bの単位時間あたりの変化
磁石と銅板の距離xが変われば、図2にあるように磁界の強さも変わります。磁束密度Bの単位時間あたりの変化
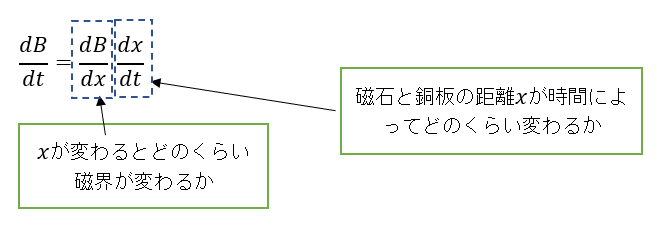
右辺の第1項は図2のカーブの傾きなので、 f(x)を微分すれば求められます。第2項は磁石の落下速度 v です。つまり銅板内に流れる渦電流の大きさは、f'(x)・v に比例するものとみなせます。ただし、f'(x)は、f(x)をxで微分した関数です。
3.2 銅板内に流れる渦電流による磁界が磁石に及ぼす力
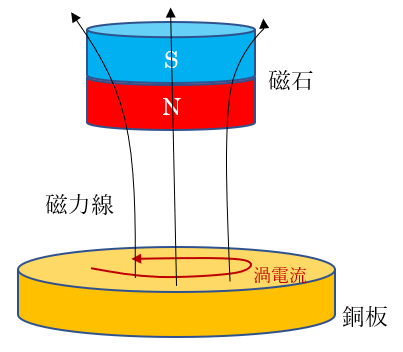 |
| 図5 銅板内に流れる渦電流の作る磁界(磁力線、渦電流はイメージ) |
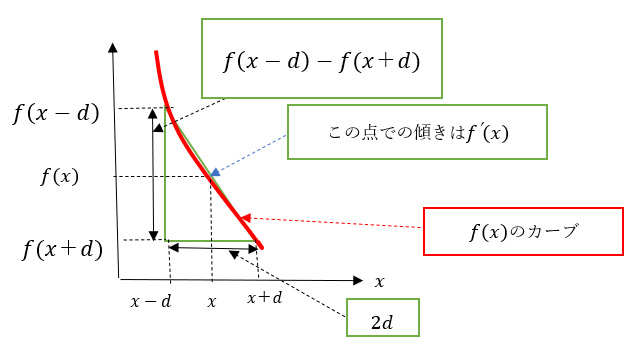
磁石の位置をx、磁石の厚みを2dとすると、N極に働く反発力はf(x-d)に比例し、S極に働く吸引力はf(x+d)に比例するものと考えられます。図6にあるように
ですので、結局、トータルとしての反発力はf’(x)に比例すると考えられます。
 |
| 図6 |
3.3 磁石に働く反発力
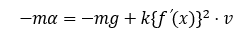
つまり加速度
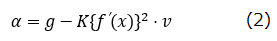
ただし、
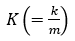 は定数です。
は定数です。4.解析結果
実験条件に合わせて、初期条件は時間 t=0[s]で、位置 x=105[㎜]、速度v=0[m/s]としました。(位置 xは銅板からの高さで表しています。)時間ステップは1[ms](=0.001[s]=1.0×10-3 [s])としました。重要なのが K の値ですが、これは厳密には、銅板内の渦電流の大きさと分布、その渦電流が空間に作る磁界分布を考慮して算出しなければなりません。しかし、その解析は非常に難解なので、ここでは簡単のため、実験結果との比較からKを0.00004として計算を行いました。(注)
計算結果が図7、図8です。 図7、図8を実験結果と比べてみれば明らかなように、実験結果とほぼ同様の特性が得られており、Kの値も含め、これまでの仮定が妥当なものであると言えます。
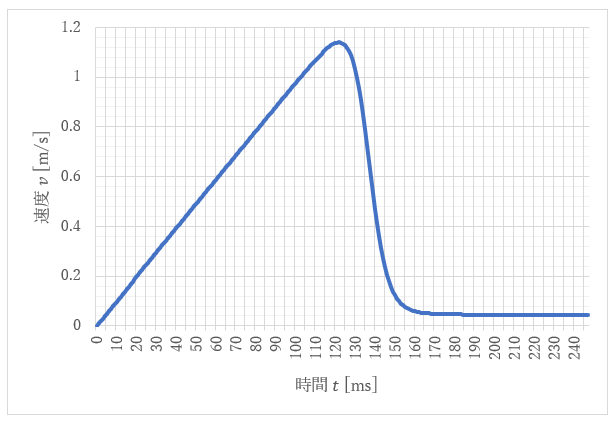 |
| 図7 落下速度の時間変化 |
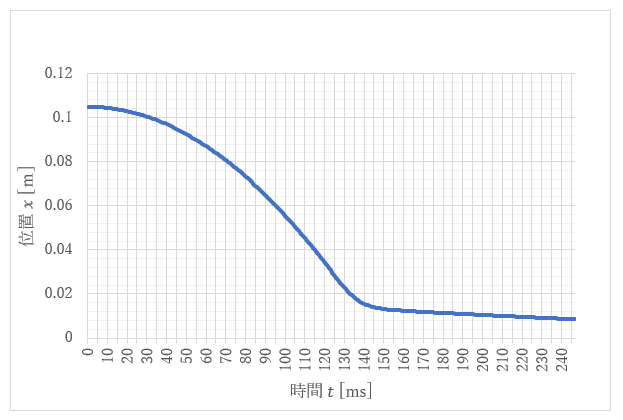 |
| 図8 磁石の位置の時間変化 |
図9は(2)式の第2項で表される反発力の大きさを磁石の位置に対して示したものです。この縦軸で9.8のところが重力と同じになります。
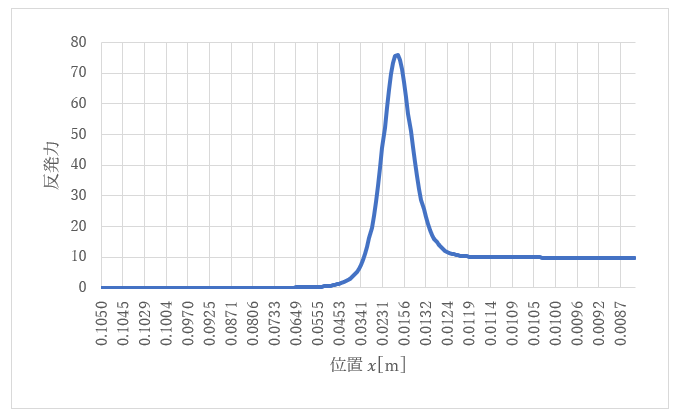 |
| 図9 磁石の位置と反発力の関係 |
銅板から1~3[㎝]の位置で、最大で重力の7倍程度の強い反発力が生じていることが判ります。この反発力で磁石の落下速度は急激に減少します。一方、銅板から1[㎝]程度に近づくと、反発力は重力と同程度になり、平衡状態となっていることが判ります。ただし平衡状態といっても磁石が空間にじっと浮かんでいるわけではなく、その直前の速度から、加速も減速もせず一定速度で落下している状態です。この速度は、それ以前よりもかなり低速ですので、「ふわっと」落ちるのです。
5.まとめ
さらに、最終段階では落下速度は非常に低速となり、ふわっと落ちることも判りました。
注)先進核融合・物理教育研究所の御手洗氏は、導体板を流れる渦電流がドーナッツ状に流れると仮定したモデルを用いて、落下する磁石の挙動の詳細な定量的解析を行われています(私信)。ただ、それはかなり複雑なモデルなので、ここでは定性的な特性の把握を目的に、簡略化したモデルを用いて検討を行いました。
謝辞
再提出 2022年3月14日
ⅰ 詳しくは、石川 「改訂電気磁気学演習」 学献社 などをごらん下さい。
ⅱ 磁界と磁束密度について、もっと詳しく知りたい方は、例えば次の本をご覧ください。
『電気磁気学[3版改訂]』 山田直平原著 桂井誠改訂著 電気学会
